Ad1
Ad2
 |
| Cara Menggunakan dan Menghitung Teorema Pythagoras |
Teorema Pythagoras berlaku segitiga siku-siku. Sisi terpanjang segitiga siku-siku, yaitu sisi yang berhadapan dengan sudut siku-siku, disebut sisi miring.
Teorema Pythagoras Menyatakan :
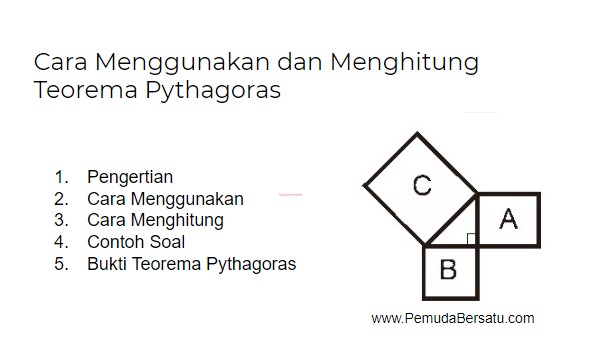
"Pada segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat dua sisi yang lain".
Liat gambar 0.1, pernyataan tersebut menjadi luas bujur sangkar C = luas bujur sangkar A + luas bujur sangkar B. Hasil pemikiran ini telah dikenal oleh bangsa Babilonia selama lebih dari empat ribu tahun yang lalu, dan di Mesir kuno, para penyigi yang dikenal sebagai 'perentang tali' mengetahui bahwa sebuah segitiga yang panjang sisi-sisinya 3, 4 dan 5 satuan memiliki sudur siku-siku di antara sisi-sisi dengan panjang 3 dan 4. Mereka menggunakan tali bersimpul untuk menandai sudut sikut-siku dilantai.
Pythagoras (sekitar 580-500 SM) atau salah satu pengikutnya, mungkin merupakan orang pertama yang membuktikan hasilnya. Phthagoras tinggal di Crotona, jajahan Yunani di Italia bagian selatan, sekitar tahun 530 SM. Di sana Pythagoras mendirikan masyarakat matematika dan filsafat yang memberikan sumbangan besar dalam bidang matematika, khususnya bilangan yang mereka beri sifat mistis dan keselarasan alat musik berdawai.
Cara Menggunakan Teorema Pythagoras.
Sebuah bukti dari teorema ini terdapat dibagian gambar 0.2, bagian berikutnya menunjukkan bagaimana cara menggunakan teorema tersebut.
Jika kamu mengetahui luas bujur sangkar yang digambar di dua sisi segitiga siku-siku, kamu dapat menggunakan teorema pythagoras untuk mencari luas bujur sangkar yang du gambar 0.3.
Misal, di gambar 0.1, jika luas bujur sangkar A 20 cm² dan luas bujur sangkar B 13 cm², luas bujur sangkar C adalah (20 + 13) cm² = 33 cm². Praktisnya, jika sudah diketahui dus sisi sebuah segitiga siku-siku, biasanya dengan menggunakan teorema Pythagoras kamu dapat menghitung panjang sisi ketiga segitiga siku-siku tersebut. Untuk tujuan ini, akan lebih berguna jika teorema tersebut dinyatakan dalam panjang sisi-sisinya, liat gambar 0.2. C² = a² + b².
Pada gambar 03, nilai a8 dan nilai b6, satuannya sentimeter. Karena c digantikan x, dengan teorema Pythagoras menjadi x² = 8² + 6² = 64 + 36 = 100. Karena x bilangan positif dan x² = 100, x = 10, jadi sisi ketiga siku-siku tersebut 10 cm.
Contoh.
Soal pertama.
Perhatikan Gambar soal 0.1. Hitunglah panjang sisi yang ditandai dengan x cm pada segitiga siku-siku disamping dalam 3 bilangan bermakna.
Jawab.
7² = x² + 4².
49 = x² + 16.
x² = 49 - 16 = 33.
x = √33 = 5,74 pembulatan tiga bilangan bermakna.
Jadi panjang sisi ketiga dalam pembulatan tiga bilangan bermakna 5,74 cm.
Kamu dapat membagi segitiga sama kaki dan sama sisi menjadi dua segitiga siku-siku dengan sebuah garis simetri kemudian gunakan teorema Pythagoras.
Baca juga. Rumus Luas Lingkaran Termudah
Soal Kedua.
Gambar soal 0.2. menunjukan segitiga sama kaki dengan alas 24 cm dan garis tinggi 9 cm. Hitunglah sisi yang ditandai dengan 1 cm.
Jawab.
Dari teorema Pythagoras pada segitiga siku-siku.
P = 12² + 9² = 144 + 81 = 225 jadi 1 = √ 225 = 15.
Panjang sisi 1 adalah 15 cm.
Jika jumlah bujur sangkar didua sisi segitiga sama dengan bujur sangkar disisi ketiga, segitiga tersebut adalah segita siku-siku.


